树的学习笔记

二叉树

基本概念

1.记录根节点的高度为0，那么一个满二叉树的结点个数为2^(h+1)-1

利用等比求和…..，最少为h+1

二叉树的实现

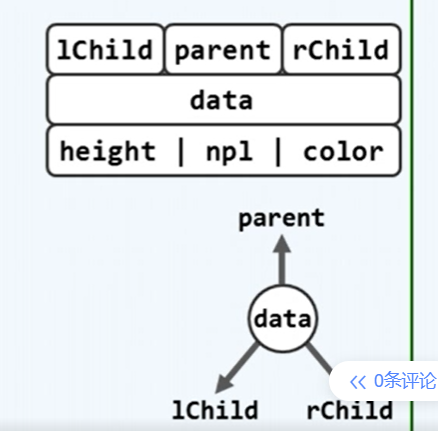
1.基本结点BinNode 模板类

#define BinNodePosi(T) BinNode<T>* //结点位置
template <typename T> struct BinNode{
    BinNodePosi(T) parent,lChild,rChild;// 父亲 孩子
    T data; int heigt;int size(); //高度 规模
    BinNodePosi(T) insertAsLC(T const &);//左孩子插入结点
    BinNodePosi(T) insertAsRC(T const &);//右孩子插入结点
    BinNodePosi(T) succ();//(中序意义下) 当前节点直接后继
    template <typename VST> void travlevel (VST &);//层次遍历
    template <typename VST> void travPre (VST &);//先序遍历
    template <typename VST> void travIn(VST &);//中序遍历
    template <typename VST> void travPost(VST &);//后续遍历
}

插入结点

template <typename T> BinNOdePosi(T) BinNode<T>::insertAsLC(T const & e){
    return lChild=new BinNode(e,this);
}

右孩子结点插入相似O(1)

size的实现

template <typename> int BinNode<T>::size(){
    int s=1;// 计入根本身
    if(lChild) s+=lChild->size();//递归计算左子树
    if(rChild) s+=rChild->size();
    return s;
}

时间复杂度O(n)

2.树 的模板类实现BinTree

template <typename T> class BinTree{
protected:
    int size; //规模
    BinNodePosi(T) root; //根节点
    virtual int updateHeight(BinNodePosi(T) x)//更新结点x的高度
public:
    int size()const{
        return size;
    }
    bool empty()const {
        return !root;
    }//判空
    BinNodePosi(T) root() const{
        return root;
    }//树根
   /* 还有一群遍历算法*/
}

高度更新

高度： 一结点到其叶子结点的最大深度（空树的高度为-1）