KMP算法
浅聊一下对KMP算法的理解吧。自认为KMP算法还是有些难理解的。
原本的暴力破解字符串匹配问题上,每发生一次不匹配情况都需要子串(t)回溯到第一个位置,然后再和主串(s)的下一位进行匹配。这种模式下,对前面已经匹配过的字符又进行了重复运算,回溯的步骤太多,造成了大量的资源浪费。这种算法下的时间复杂度 达到了O(m*n)。
- 最长相等前后缀
在讲KMP算法前,需要引入一个前后缀概念
如abcab,最长前后缀是ab,长度为2
再如a b c d e a b c 最长前后缀是abc,长度为3
相信这个概念通过这两个例子还是很好理解的。
- KMP算法原理
在有了最长相等前后缀这个概念之后,我们就可以聊一聊KMP算法是如何实现的了
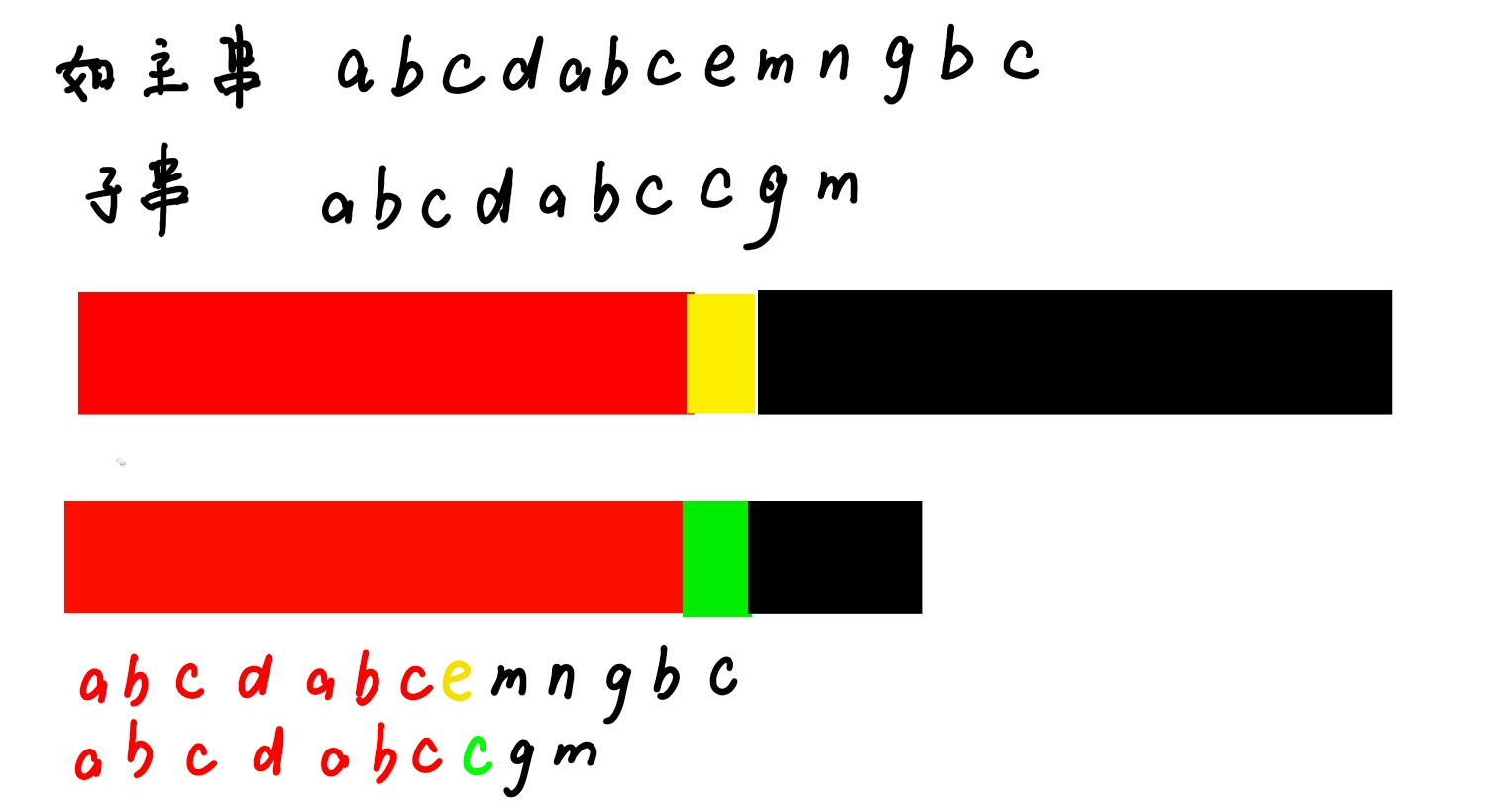
对于已经进行匹配的字符串而言,最长前后缀是abc(蓝色),长度为3.
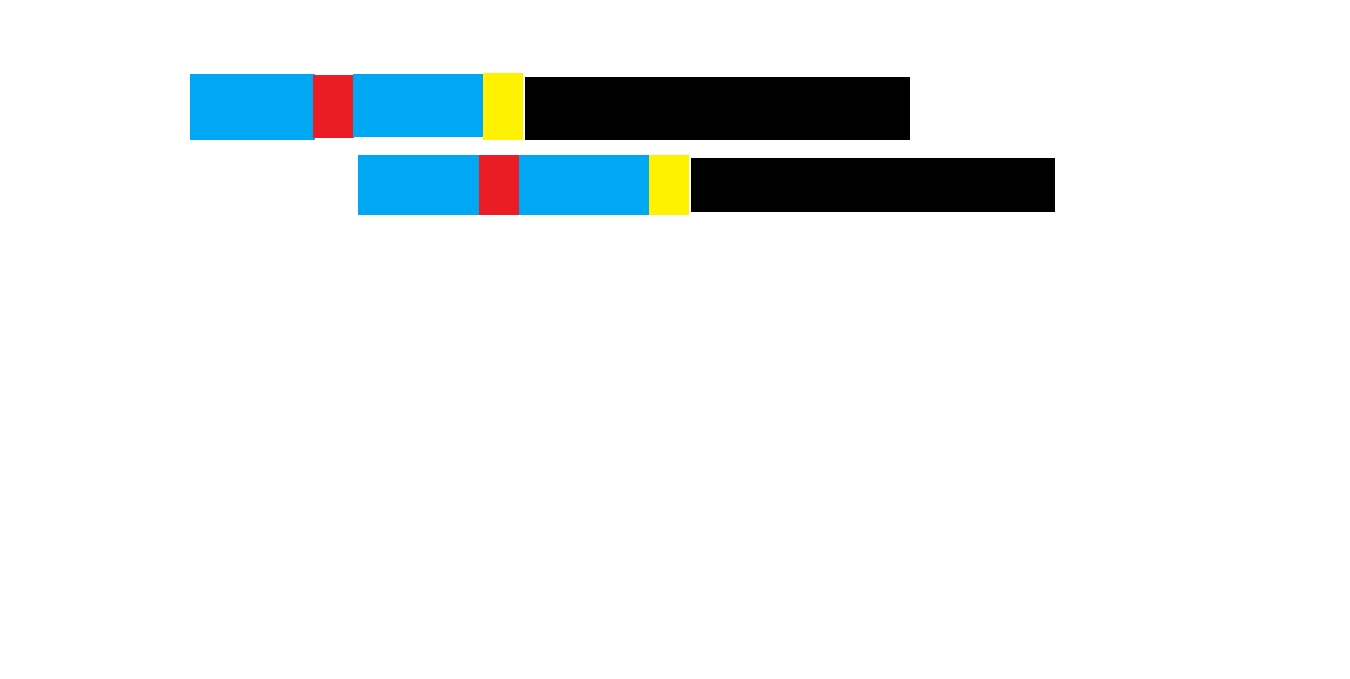
根据KMP算法原理,我们需要将子串向后移动再进行比较,移动结果就是将子串的最长相等前缀移动到主串的最长相等后缀的位置上。这基本上就是KMP算法的原理。
移位的实现
1.next[i]数组的含义
next[i]的值表示下标为i的字符前的字符串最长相等前后缀的长度。
同时next[i]也是在i处不匹配后,子串应该回溯到的位置,也就是t[next[i]]
对于原例来讲,其next[]数组的值如下
| a | b | c | d | a | b | c | c | g | m |
|---|---|---|---|---|---|---|---|---|---|
| next[0] | next[1] | next[2] | next[3] | next[4] | next[5] | next[6] | next[7] | next[8] | next[9] |
| -1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 0 | 0 |
2.next[i]的代码实现及图解
2.1. 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
typedef struct
{
char data[MaxSize];
int length; //串长
} SqString; //串的结构体定义
void GetNext(SqString t,int next[i]){
int j=0,k=-1;
int next[0]=-1; //初始化
while(j<t.length-1)// 每一次对next[]赋值都是发生在j++之后
if(k==-1||t.data[j]==t.data[k]){
k++,j++;
next[j]=k;
}
//如果在k位置和j位置上的字符串相匹配,则红色区域,也就是前后缀长度+1
else{
k=next[k];
}/*这一步感觉是有些难的。
我们已知next[k]代表的是在k位置前的最长前后缀的长度
那么如果出现字符串不匹配的情况,我们就需要在红色部分
也就是原有的最长前缀里再寻找相等前后缀
那么t.data[k]就是原有的红色部分里继续开始寻找前后缀
的位置*/
}
2.2.图解
这里就直接引用网上的图解了,感觉还是比较清晰的。
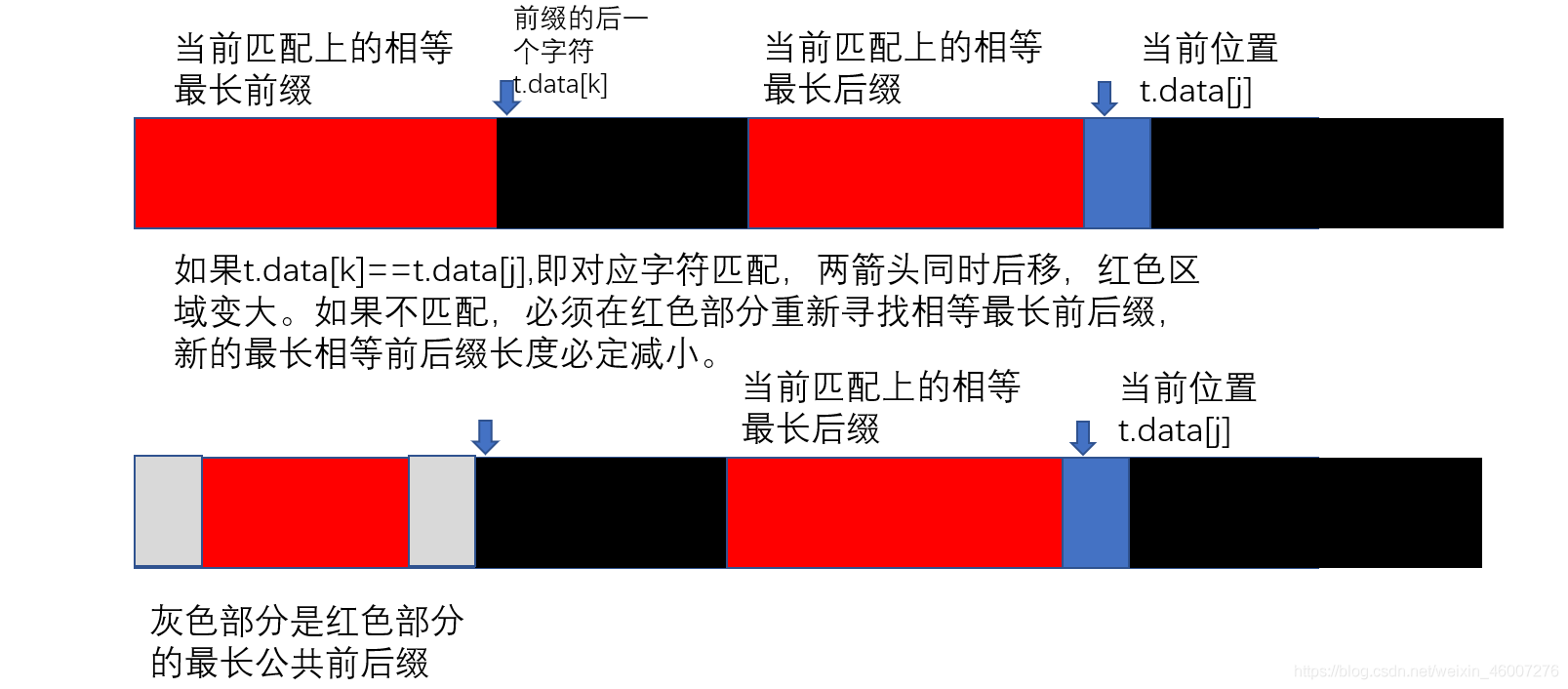
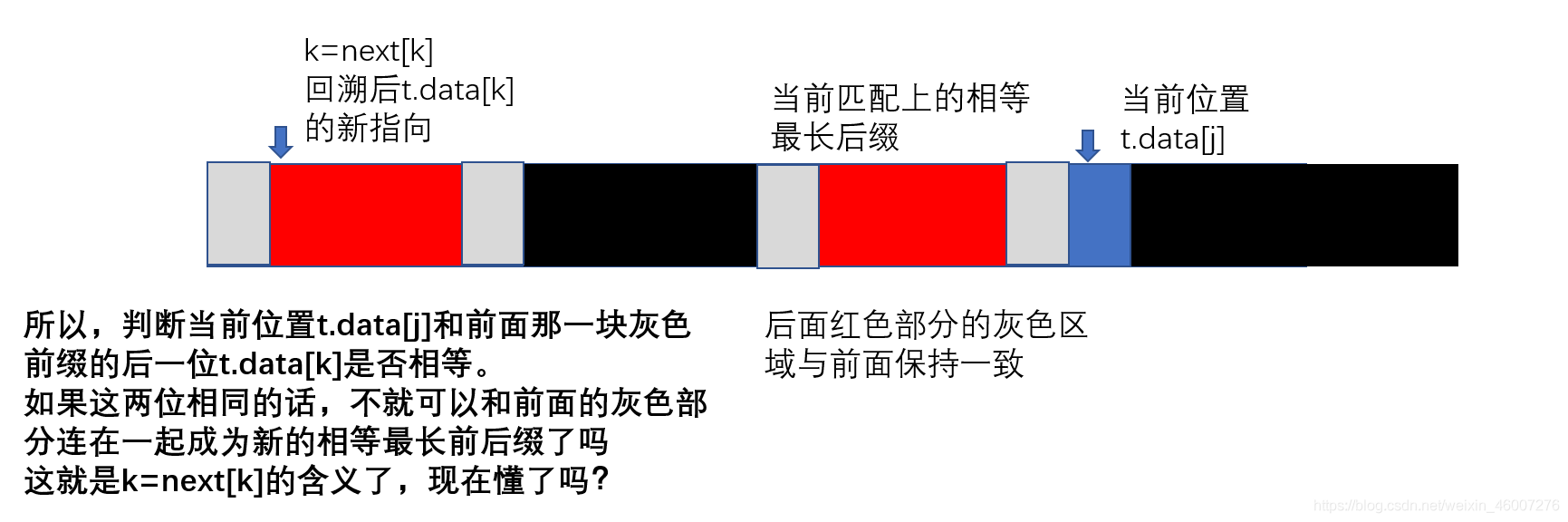
KMP 算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int KMPIndex(SqString s,SqString t)
{
int next[MaxSize],i=0,j=0;
GetNext(t,next);
while (i<s.length && j<t.length)
{
if (j==-1 || s.data[i]==t.data[j])
{
i++;j++; //i,j各增1
}
else j=next[j]; //主串i位置不变,子串以最长前后缀长度为 回溯长度
}
if (j>=t.length)
return(i-t.length); //返回匹配模式串的首字符下标
else
return(-1); //返回不匹配标志
}